求cos(x)级数的C程序

我们给出 x 和 n 的值，其中 x 是 cos 的角度，n 是 cos(x) 级数中的项数。

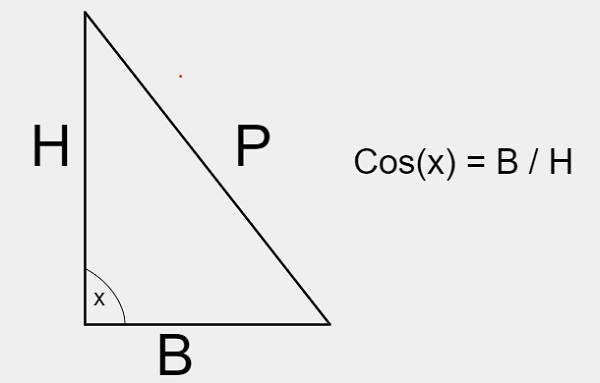
对于 Cos(x) h3>

Cos(x)是一个三角函数，用于计算x角度的值。

公式

$$\cos (x) = \displaystyle\sum\limits_{k=0} ^\infty \frac{(-1)^{k}}{(2k!)}x^{2k}$$

同徽B2B电子商务软件 V46

同徽B2B电子商务软件是国内第一个基于J2EE架构的电子商务商业程序，在国内同类软件中市场占有率位居第一。目前客户分布二十多个省份，三十几个行业，直接和间接服务500万企业,其中包括多家部级单位和世界500强企业：商务部、农业部、德赛集团、宝钢集团、江苏龙华集团、深圳中农股份、中集集团等。 。 网站参数管理运营商可对整个网站进行灵活的配置，适应不同的运营需求网站更新将信息生成静态页面，加快浏览速

下载

对于 Cos(x) 级数

Cos( x) = 1 – (x*2 / 2!) + (x*4 / 4!) – (x*6 / 6!) + (x*8 / 8!)……

示例

Input-: x = 10, n = 3
Output-: 0.984804
Input-: x = 8, n = 2
Output-: 0.990266

下面程序中使用的方法如下 -

• 输入x和n的值
• 应用cos(x)级数的计算公式
• 打印结果作为所有级数的总和

算法

Start
Step 1 Declare and initialize const double PI = 3.142
Step 2 In function double series_sum(double x, int n)
   Set x = x * (PI / 180.0)
Set result = 1
Set s = 1, fact = 1, pow = 1
    Loop For i = 1 and i < 5 and i++
        Set s = s * -1
        Set fact = fact * (2 * i - 1) * (2 * i)
        Set pow = pow * x * x
        Set result = result + s * pow / fact
     End Loop
    Return result
Step 3 In function int main() s
    Declare and set x = 10
Declare and set n = 3
    Print series_sum(x, n)  
Stop

示例

#include 
const double PI = 3.142;
//will return the sum of cos(x)
double series_sum(double x, int n) {
    x = x * (PI / 180.0);
    double result = 1;
    double s = 1, fact = 1, pow = 1;
    for (int i = 1; i < 5; i++) {
        s = s * -1;
        fact = fact * (2 * i - 1) * (2 * i);
        pow = pow * x * x;
        result = result + s * pow / fact;
    }
    return result;
}
//main function
int main() {
    float x = 10;
    int n = 3;
    printf("%lf
", series_sum(x, n));  
    return 0;
}

输出

X=10; n=30.984804
X=13; n=80.974363
X=8; n=2 0.990266