满射与满秩的关系取决于矩阵维度:当行数m≤列数n时,满秩(rank=min(m,n)=m)等价于满射(rank=m);当m>n时,满秩(rank=n)无法满足满射(需rank=m),故不等价。
线性代数中,一个线性变换如果是“满射”,意味着它的像(输出空间)能够完全覆盖其协同域。而矩阵的“满秩”,则表示其秩达到了行数和列数中的较小值。两者的关系可以这样概括:对于一个将n维空间映射到m维空间的线性变换,如果它是满射的,那么它对应的m x n矩阵必然具有满行秩(即秩等于m)。当且仅当矩阵的行数m小于或等于列数n时,满行秩才等同于我们通常所说的“满秩”(即秩等于min(m, n))。所以,在特定条件下,满射与满秩是紧密关联甚至等价的。
解决方案
要深入理解线性代数中满射(Surjectivity)与满秩(Full Rank)的关系,我们得从它们各自的定义入手,然后观察它们在矩阵表示下的交集。
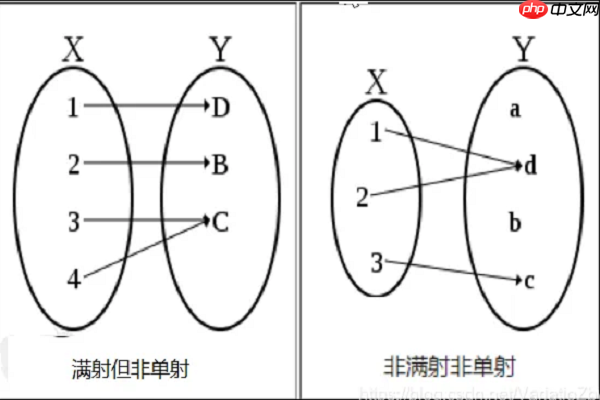
一个从向量空间V到向量空间W的线性变换T: V → W被称为满射,如果对于W中的每一个向量w,在V中都存在至少一个向量v,使得T(v) = w。简单来说,就是变换的“输出”能够覆盖整个“目标空间”W,没有任何一个W中的元素是T触及不到的。
当我们将这个线性变换T用一个m x n的矩阵A来表示时,其中m是W的维度,n是V的维度,那么T的像(Image of T)就是A的列空间(Column Space of A)。因此,T是满射的,当且仅当A的列空间能够张成整个m维空间R^m。这意味着A的列空间的维度必须等于m,即 rank(A) = m。
现在来看“满秩”。一个m x n的矩阵A被称为满秩,如果它的秩(rank)等于min(m, n)。秩是矩阵列空间(或行空间)的维度,它代表了矩阵所能承载的线性独立信息的最大数量。
那么,两者的关系就清晰了:
- 满射条件:要求 rank(A) = m (即矩阵A具有满行秩)。
- 满秩条件:要求 rank(A) = min(m, n)。
- 如果 m :在这种情况下,min(m, n) = m。所以,如果A是满秩的(rank(A) = m),那么它也满足满射的条件(rank(A) = m)。反之,如果A是满射的(rank(A) = m),那么它也满足满秩的条件(rank(A) = m = min(m, n))。因此,当行数不大于列数时,满射与满秩是等价的。
- 如果 m > n:在这种情况下,min(m, n) = n。如果A是满秩的,意味着 rank(A) = n。然而,满射的条件是 rank(A) = m。由于 m > n,所以 rank(A) = n 不可能等于 m。这意味着,当行数大于列数时,一个矩阵即使是满秩的,它也绝不可能是满射的。实际上,在这种情况下,满射是不可能发生的,因为你试图用n个向量去张成一个m维空间(m>n),这是不可能做到的。
所以,一个线性变换是满射的,等价于其表示矩阵具有满行秩。而“满秩”这个概念,只有在矩阵的行数不大于列数时,才与满射直接关联。
为什么线性代数中的满射概念在数据处理与机器学习中至关重要?
在数据处理和机器学习的语境下,满射这个概念,虽然听起来有点抽象,但实际上它渗透在我们处理数据、构建模型的核心逻辑里。我个人觉得,它的重要性主要体现在几个方面:
首先,数据覆盖与信息完备性。想象一下,你有一个高维的原始数据集(比如图像的像素值),你想通过某种特征提取或降维方法,将其映射到一个较低维度的特征空间。如果这个映射是满射的,它意味着你的特征空间中的每一个可能的“点”或“状态”,都能被原始数据中的某个组合所生成。这在某种程度上保证了你的特征表示是“全面”的,没有遗漏掉目标空间中的任何一个“可能性”。虽然在降维时,我们通常是从高维到低维,不太可能严格意义上的满射(除非低维空间被高维空间完全覆盖,且维度一致),但满射的思想提醒我们,要确保特征能尽可能地捕捉和表达目标空间的所有变化。
其次,模型输出的表达能力。在机器学习中,特别是分类任务,模型的最后一层通常会输出一个向量,这个向量代表了输入属于各个类别的概率或得分。如果你的模型输出层所能产生的向量集合,不能完全覆盖所有可能的类别组合(或者说,它无法输出某种特定的分类结果),那么这个模型就不是“满射”的。这意味着你的模型有内在的局限性,它可能永远无法正确预测某些边缘或罕见的分类情况,因为它根本无法“生成”那种输出。一个具有满射能力的输出层,理论上能够表达任何可能的分类结果,从而提供了更强的模型表达力。
再者,系统可控性与可达性。在更广义的系统理论中,满射与“可达性”紧密相关。如果一个动态系统是满射的,意味着通过适当的输入,可以使系统达到其所有可能的状态。这在控制系统设计中至关重要,比如机器人路径规划,你希望机器人能到达工作空间中的任何一点。在数据流或管道设计中,如果某个处理步骤是满射的,意味着它不会“阻塞”下游对某些特定类型数据的需求。
最后,线性方程组的可解性。这是最直接也最基础的应用。如果一个线性系统 Ax = b 对应的矩阵 A 是满射的(即满行秩),那么对于任何给定的b,这个方程组都必然有解。这在数据建模中意味着,你的模型(A)总能找到一组参数(x)来拟合任何观测数据(b),这为模型的鲁棒性和泛化能力提供了基础保障。
如何判断一个线性变换或矩阵是否具有满射性?
判断一个线性变换或矩阵是否具有满射性,其实有很多种方法,它们殊途同归,都是在验证其“覆盖”能力。我通常会根据具体情况选择最便捷的一种:
-
检查矩阵的秩(Rank): 这是最直接也是最常用的方法。对于一个从R^n到R^m的线性变换T,如果它由一个m x n的矩阵A表示,那么T是满射的当且仅当A的秩等于m(即 rank(A) = m)。
- 操作方法:将矩阵A进行行简化(高斯消元),得到它的行阶梯形(Row Echelon Form)或简化行阶梯形(Reduced Row Echelon Form)。计算主元(leading ones)的数量。如果主元的数量等于矩阵的行数m,那么矩阵A就是满行秩的,对应的线性变换就是满射的。
- 例子: 一个 2x3 矩阵 $A = \begin{pmatrix} 1 & 2 & 3 \ 4 & 5 & 6 \end{pmatrix}$。 进行行简化后,可以得到类似 $\begin{pmatrix} 1 & 0 & -1 \ 0 & 1 & 2 \end{pmatrix}$。 这里主元数量是2,矩阵行数也是2。所以 rank(A) = 2 = m,这个变换是满射的。
-
检查列向量是否张成协同域: 满射意味着矩阵的列空间(由列向量张成的空间)必须等于整个协同域R^m。
- 操作方法:取出矩阵A的所有列向量。判断这些列向量是否能张成R^m。这通常也通过高斯消元来完成:将这些列向量看作一个增广矩阵的系数部分,或者直接看它们是否包含m个线性无关的向量,并且这些向量能够构成R^m的一个基。
- 例子: 对于上面的2x3矩阵A,它的列向量是 $\begin{pmatrix} 1 \ 4 \end{pmatrix}$, $\begin{pmatrix} 2 \ 5 \end{pmatrix}$, $\begin{pmatrix} 3 \ 6 \end{pmatrix}$。 我们只需要找到其中2个线性无关的向量就能张成R^2。比如 $\begin{pmatrix} 1 \ 4 \end{pmatrix}$ 和 $\begin{pmatrix} 2 \ 5 \end{pmatrix}$ 显然是线性无关的。所以,这些列向量张成了R^2,变换是满射的。
-
对于方阵(m=n)的情况,检查行列式: 如果矩阵A是方阵(m x m),那么T是满射的当且仅当A是可逆的。而可逆性可以通过计算行列式来判断。
- 操作方法:计算 det(A)。如果 det(A) ≠ 0,那么A是可逆的,T就是满射的。
- 例子: 一个 2x2 矩阵 $B = \begin{pmatrix} 1 & 2 \ 3 & 4 \end{pmatrix}$。 det(B) = (14) - (23) = 4 - 6 = -2 ≠ 0。 所以B是可逆的,对应的变换是满射的。
-
是否存在右逆矩阵: 一个线性变换T: V → W是满射的,当且仅当存在一个线性变换S: W → V,使得T S = I_W(W上的恒等变换)。对于矩阵而言,这意味着m x n矩阵A是满射的,当且仅当存在一个n x m矩阵B,使得AB = I_m(m x m的单位矩阵)。这个B被称为A的右逆矩阵。
- 操作方法:尝试构造或证明右逆矩阵的存在。这通常也归结为判断A是否具有满行秩。
在实际操作中,计算矩阵的秩通常是最直接和最可靠的方法,因为它适用于任何维度的矩阵,并且高斯消元法是一个非常标准化的过程。
满秩矩阵是否总是意味着满射?反之亦然?
这是一个非常好的问题,它触及了满秩和满射概念的细微差别,尤其是在非方阵的情况下。答案是:不总是。我们需要分情况讨论。
首先,我们再次明确定义:
- 满射(Surjective):对于一个m x n矩阵A,表示一个从R^n到R^m的线性变换。如果它是满射的,意味着它的秩等于协同域的维度,即 rank(A) = m。这有时也被称为“满行秩”。
- 满秩(Full Rank):对于一个m x n矩阵A,如果它的秩等于其行数和列数中的较小者,即 rank(A) = min(m, n)。
现在,我们来看不同情况:
1. 矩阵的行数小于或等于列数 (m ≤ n)
在这种情况下,min(m, n) = m。
-
满秩是否意味着满射? 是的。 如果矩阵A是满秩的,那么 rank(A) = min(m, n) = m。这正好满足了满射的条件 rank(A) = m。 所以,当 m ≤ n 时,一个满秩矩阵必然是满射的。
- 例子:一个 2x3 矩阵 $A = \begin{pmatrix} 1 & 2 & 3 \ 4 & 5 & 6 \end{pmatrix}$。它的秩是2。 这里 m=2, n=3。min(m, n) = 2。 因为 rank(A) = 2 = min(m, n),所以A是满秩的。 同时,因为 rank(A) = 2 = m,所以A也是满射的。
-
满射是否意味着满秩? 是的。 如果矩阵A是满射的,那么 rank(A) = m。 由于我们处于 m ≤ n 的情况,所以 m = min(m, n)。因此 rank(A) = m = min(m, n),这满足了满秩的条件。 所以,当 m ≤ n 时,一个满射矩阵必然是满秩的。
- 结论:当行数不大于列数时,满秩和满射是等价的。
2. 矩阵的行数大于列数 (m > n)
在这种情况下,min(m, n) = n。
-
满秩是否意味着满射? 否。 如果矩阵A是满秩的,那么 rank(A) = min(m, n) = n。 然而,满射的条件是 rank(A) = m。由于 m > n,所以 rank(A) = n 绝不可能等于 m。 因此,当 m > n 时,一个满秩矩阵不可能是满射的。实际上,在这种情况下,任何线性变换都不可能是满射的,因为你试图用n个向量(列)去张成一个m维空间,而n
- 例子:一个 3x2 矩阵 $B = \begin{pmatrix} 1 & 2 \ 3 & 4 \ 5 & 6 \end{pmatrix}$。它的秩是2。 这里 m=3, n=2。min(m, n) = 2。 因为 rank(B) = 2 = min(m, n),所以B是满秩的。 但是,因为 rank(B) = 2 ≠ m (m=3),所以B不是满射的。它只能将R^2映射到R^3中的一个2维子空间。
满射是否意味着满秩? 否(实际上在这种情况下,满射是不可能的)。 如果矩阵A是满射的,那么 rank(A) = m。 但我们知道,矩阵的秩不可能超过它的列数,即 rank(A) ≤ n。 由于我们处于 m > n 的情况,所以 rank(A) = m 与 rank(A) ≤ n 矛盾。 这意味着,当 m > n 时,不存在满射的线性变换。
总结:
- 满秩不总是意味着满射:只有当矩阵的行数小于或等于列数 (m ≤ n) 时,满秩才意味着满射。当行数大于列数 (m > n) 时,满秩矩阵不可能是满射的。
- 满射不总是意味着满秩:当 m ≤ n 时,满射确实意味着满秩。但当 m > n 时,满射是不可能发生的。
所以,更准确的说法是:一个线性变换是满射的,当且仅当其表示矩阵具有满行秩(即秩等于行数m)。而“满秩”这个术语,只有在行数不大于列数时,才与满射的概念直接重合。






























