2699。修改图边权重
难度:难
主题:图、堆(优先级队列)、最短路径
给你一个无向加权连通图,其中包含标记为0到n - 1的n个节点,以及一个整数数组edges,其中edges[i] = [ai, b i, wi] 表示节点 ai 和 bi 之间有一条边,权重为 wi.
某些边的权重为 -1 (wi = -1),而其他边的权重为 正 (wi > 0)。
你的任务是修改所有边的权重为-1,方法是在[1, 2 * 109范围内分配正整数值 ] 使得节点源和目的地之间的最短距离变得等于整数目标。如果有多次修改使源和目的地之间的最短距离等于目标,则其中任何一个都将被视为正确。
如果可以使从源到目的地的最短距离等于目标,则返回以任意顺序包含所有边(甚至未修改的边)的数组,如果不可能,则返回空数组 .
注意:不允许修改初始为正权重的边的权重。
示例1:
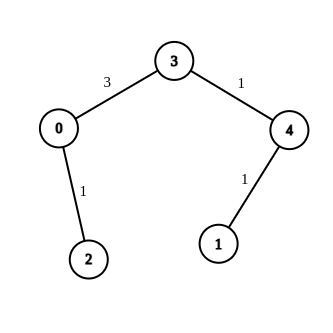
- 输入: n = 5,边 = [[4,1,-1],[2,0,-1],[0,3,-1],[4,3,-1] ],源 = 0,目的地 = 1,目标 = 5
- 输出: [[4,1,1],[2,0,1],[0,3,3],[4,3,1]]
- 解释:上图显示了对边缘的可能修改,使得从 0 到 1 的距离等于 5。
示例2:
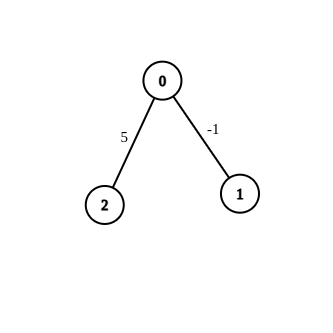
- 输入: n = 3,边 = [[0,1,-1],[0,2,5]],源 = 0,目的地 = 2,目标 = 6
- 输出: []
- 解释: 上图包含初始边。通过修改权重-1的边是不可能使从0到2的距离等于6的。因此,返回一个空数组。
示例 3:
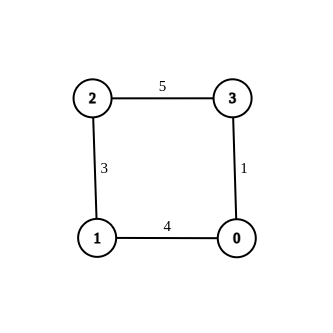
- 输入: n = 4,边 = [[1,0,4],[1,2,3],[2,3,5],[0,3,-1]],源= 0,目的地 = 2,目标 = 6
- 输出: [[1,0,4],[1,2,3],[2,3,5],[0,3,1]]
- 解释:上图显示了修改后的图,其中从 0 到 2 的最短距离为 6。
约束:

2088shop商城购物系统是商城系统中功能最全的一个版本:非会员购物、商品无限级分类、不限商品数量、商品多级会员定价、上货库存、Word在线编辑器、订单详情销售报表、商品评论、留言簿、管理员多级别、VIP积分、会员注册积分奖励、智能新闻发布、滚动公告、投票调查、背景图片颜色更换、店标上传、版权联系方式修改、背景音乐(好歌不断)、广告图片支持Flash、弹出浮动广告、搜索引擎关健词优化、图文友情联
- 1
- 1
- 边[i].length == 3
- 0 i, bi
- wi = -1 或 1 i 7
- ai != bi
- 0
- 来源!=目的地
- 1 9
- 图是连通的,不存在自环或重复边
提示:
- 首先,检查是否确实可以使从源到目的地的最短路径等于目标。
- 如果在没有修改边的情况下从源到目的地的最短路径小于目标,则这是不可能的。
- 如果从源到目的地的最短路径(包括要修改的边并为其分配临时权重 1)大于目标,那么它也是不可能的。
- 假设我们可以找到一条可修改的边 (u, v),使得从源到 u 的最短路径长度 (dis1) 加上从 v 到目的地的最短路径长度 (dis2) 小于目标 (dis1) + dis2
- 对于所有其他仍具有权重“-1”的边,将权重更改为足够大的数字(目标、目标 + 1 或 200000000 等)。
解决方案:
我们可以将方法分解如下:
方法:
-
对现有权重进行初步检查:
- 首先,我们仅使用权重为正的边计算从源到目的地的最短路径,忽略权重为 -1 的边。
- 如果这个距离已经大于目标,那么就不可能修改-1边来达到目标,所以我们返回一个空数组。
-
临时分配权重 1:
- 接下来,为所有权重为-1的边分配临时权重1,并重新计算最短路径。
- 如果这个最短路径仍然大于目标,那么就不可能达到目标,所以我们返回一个空数组。
-
修改特定边权重:
- 迭代权重为-1的边缘并识别可以调整以完全匹配目标距离的边缘。这是通过调整边缘的权重来完成的,这样往返于该边缘的路径的组合距离就可以得出准确的目标距离。
- 对于任何剩余的 -1 边,分配足够大的权重(例如 2 * 10^9)以确保它们不会影响最短路径。
-
返回修改后的边:
- 最后,返回修改后的边列表。
让我们用 php 实现这个解决方案:2699。修改图边权重
解释:
- dijkstra 函数计算从源到所有其他节点的最短路径。
- 我们最初计算忽略 -1 条边的最短路径。
- 如果没有-1边的路径小于目标,函数返回一个空数组,表明无法调整权重以满足目标。
- 否则,我们暂时将所有 -1 边设置为 1,并检查最短路径是否超过目标。
- 如果是,则再次无法到达目标,我们返回一个空数组。
- 然后我们策略性地修改-1边的权重,以实现精确目标的最短路径。
这种方法可以有效地检查和调整边缘权重,确保尽可能满足目标距离。
联系链接
如果您发现本系列有帮助,请考虑在 github 上给存储库 一颗星,或在您最喜欢的社交网络上分享该帖子?。您的支持对我来说意义重大!
如果您想要更多类似的有用内容,请随时关注我:
- 领英
- github





























