图的深度优先搜索从图中的一个顶点开始，在回溯之前尽可能访问图中的所有顶点。
图的深度优先搜索类似于树遍历，树遍历中讨论的树的深度优先搜索。对于树，搜索从根开始。在图中，搜索可以从任何顶点开始。
深度优先搜索树首先访问根，然后递归访问根的子树。类似地，图的深度优先搜索首先访问一个顶点，然后递归地访问与该顶点相邻的所有顶点。不同之处在于该图可能包含循环，这可能导致无限递归。为了避免这个问题，你需要跟踪已经访问过的顶点。
该搜索被称为深度优先，因为它尽可能在图中搜索“更深”。搜索从某个顶点 v 开始。访问完 v 后，它会访问 v 的未访问的邻居。如果 v 没有未访问的邻居，则搜索回溯到到达 v 的顶点。我们假设图是连通的，并且搜索开始从任何顶点都可以到达所有顶点。
深度优先搜索算法
深度优先搜索的算法在下面的代码中描述。
输入：g = (v, e) 和起始顶点 v
输出：一棵以 v 为根的 dfs 树
1 树 dfs（顶点 v）{
2 访问 v；
v 的每个邻居 w 为 3 个
4 if (w 还没有被访问过) {
5 将 v 设置为树中 w 的父级；
6 dfs(w)；
7 }
8 }
您可以使用名为
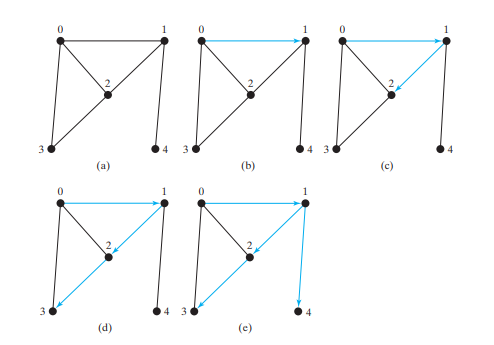
的数组来表示某个顶点是否已被访问。最初，对于每个顶点 i，isvisited[i] 为false。一旦访问了某个顶点（例如 v），isvisited[v] 就会设置为 true. 考虑下图 (a) 中的图表。假设我们从顶点 0 开始深度优先搜索。首先访问 0，然后访问它的任何邻居，比如 1。现在访问 1，如下图 (b) 所示。顶点 1 有三个邻居：0、2 和 4。由于 0 已经被访问过，因此您将访问 2 或 4。让我们选择 2。现在 2 被访问，如下图 (c) 所示。顶点 2 有 3 个邻居：0、1 和 3。由于 0 和 1 已经被访问过，所以选择 3。现在访问 3，如下图 (d) 所示。至此，顶点已按以下顺序被访问过：
、1、2、3 由于 3 的所有邻居都被访问过，所以回溯到 2。由于 2 的所有顶点都被访问过，所以回溯到 1。4 与 1 相邻，但 4 还没有被访问过。因此，访问4，如下图(e)所示。由于 4 的所有邻居都已访问过，因此回溯到 1。
由于 1 的所有邻居都已访问过，所以回溯到 0。由于 0 的所有邻居都已访问过，因此搜索结束。
由于每条边和每个顶点仅被访问一次，因此
方法的时间复杂度为o(|e| + |v|)，其中|e|表示边数，|v | 顶点数量。 深度优先搜索的实现
上面代码中的dfs算法使用了递归。很自然地使用递归来实现它。或者，您可以使用堆栈。
dfs(int v)方法在 abstractgraph.java 中的第 164-193 行实现。它返回 tree 类的实例，以顶点 v 作为根。该方法将搜索到的顶点存储在列表searchorder（第165行）中，将每个顶点的父级存储在数组parent（第166行）中，并使用isvisited数组来指示某个顶点是否已被访问（第166行） 171）。它调用辅助方法 dfs(v,parent, searchorder, isvisited) 来执行深度优先搜索（第 174 行）。 在递归辅助方法中，搜索从顶点
u开始。 u 在第 184 行添加到 searchorder 并标记为已访问（第 185 行）。对于u的每个未访问的邻居，递归调用该方法来执行深度优先搜索。当访问顶点e.v时，e.v的父顶点存储在parent[e.v]中（第189行）。当访问连通图或连通组件中的所有顶点时，该方法返回。
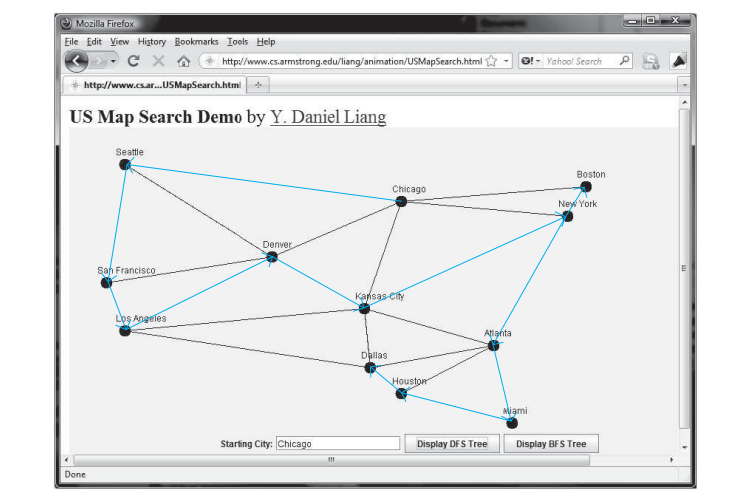
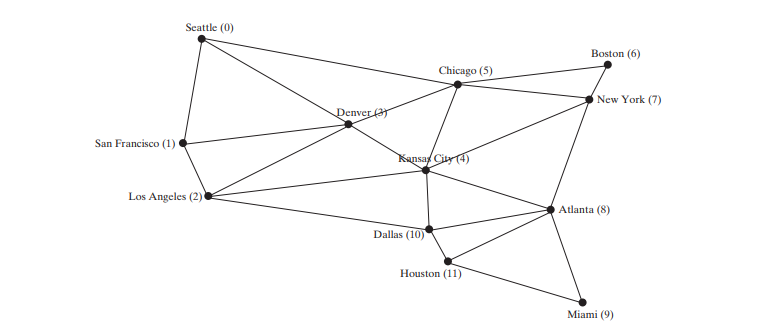下面的代码给出了一个测试程序，显示上图中从芝加哥开始的图的 dfs。从芝加哥出发的dfs示意图如下图所示
public class TestDFS {
public static void main(String[] args) {
String[] vertices = {"Seattle", "San Francisco", "Los Angeles", "Denver", "Kansas City", "Chicago", "Boston", "New York", "Atlanta", "Miami", "Dallas", "Houston"};
int[][] edges = {
{0, 1}, {0, 3}, {0, 5},
{1, 0}, {1, 2}, {1, 3},
{2, 1}, {2, 3}, {2, 4}, {2, 10},
{3, 0}, {3, 1}, {3, 2}, {3, 4}, {3, 5},
{4, 2}, {4, 3}, {4, 5}, {4, 7}, {4, 8}, {4, 10},
{5, 0}, {5, 3}, {5, 4}, {5, 6}, {5, 7},
{6, 5}, {6, 7},
{7, 4}, {7, 5}, {7, 6}, {7, 8},
{8, 4}, {8, 7}, {8, 9}, {8, 10}, {8, 11},
{9, 8}, {9, 11},
{10, 2}, {10, 4}, {10, 8}, {10, 11},
{11, 8}, {11, 9}, {11, 10}
};
Graph graph = new UnweightedGraph<>(vertices, edges);
AbstractGraph.Tree dfs = graph.dfs(graph.getIndex("Chicago"));
java.util.List searchOrders = dfs.getSearchOrder();
System.out.println(dfs.getNumberOfVerticesFound() + " vertices are searched in this DFS order:");
for(int i = 0; i < searchOrders.size(); i++)
System.out.print(graph.getVertex(searchOrders.get(i)) + " ");
System.out.println();
for(int i = 0; i < searchOrders.size(); i++)
if(dfs.getParent(i) != -1)
System.out.println("parent of " + graph.getVertex(i) + " is " + graph.getVertex(dfs.getParent(i)));
}
}
在此 dfs 顺序中搜索 12 个顶点： 芝加哥 西雅图 旧金山 洛杉矶 丹佛
堪萨斯城 纽约 波士顿 亚特兰大 迈阿密 休斯顿 达拉斯
西雅图的父母是芝加哥
旧金山的父母是西雅图
洛杉矶的父母是旧金山
丹佛的父母是洛杉矶
堪萨斯城的父母是丹佛
波士顿的父母是纽约
纽约的父母是堪萨斯城
亚特兰大的父母是纽约
迈阿密的父母是亚特兰大
达拉斯的父母是休斯顿
休斯顿的父母是迈阿密
dfs的应用
深度优先搜索可以用来解决很多问题，例如：
检测图是否连通。从任意顶点开始搜索图。如果搜索到的顶点数与图中的顶点数相同，则该图是连通的。否则，图形未连接。
- 检测两个顶点之间是否存在路径。
- 寻找两个顶点之间的路径。
- 找到所有连接的组件。连通分量是最大连通子图，其中每对顶点都通过路径连接。
- 检测图中是否存在环路。
- 在图中找到一个循环。
- 找到哈密顿路径/循环。图中的 哈密尔顿路径
- 是只访问图中每个顶点一次的路径。 哈密尔顿循环 只访问图中的每个顶点一次，然后返回到起始顶点。 前六个问题可以使用abstractgraph.java中的dfs方法轻松解决。要找到哈密顿路径/循环，您必须探索所有可能的 dfs，以找到通向最长路径的路径。哈密顿路径/循环有很多应用，包括解决著名的骑士之旅问题。
