近年来基于图的机器学习有了很大的发展。基于图的方法在数据科学中的许多常见问题中都有应用,例如链接预测、社群发现、节点分类等。根据如何组织问题和所拥有的数据,有许多解决问题的方法。本文将提供一个基于图的嵌入算法的高层次的概述。最后还将介绍如何用Python库(如node2vec)来在图上生成各种嵌入。
☞☞☞AI 智能聊天, 问答助手, AI 智能搜索, 免费无限量使用 DeepSeek R1 模型☜☜☜
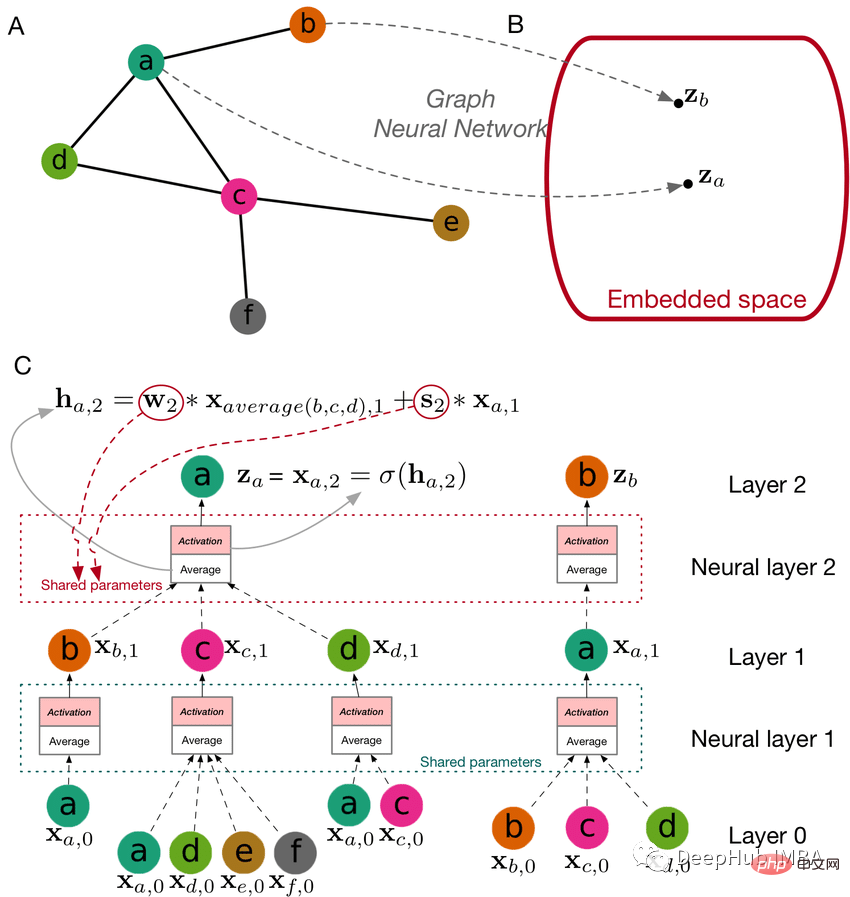
基于图的机器学习
人工智能有各种分支,从推荐系统、时间序列、自然语言处理、计算机视觉、图机器学习等。有多种方法可以通过基于图的机器学习来解决常见问题。包括社群发现、链接预测、节点分类等。
与图机器学习的一个主要问题是找到一种表示(或编码)图结构的方法,以便机器学习模型可以轻松地利用它[1]。一般情况下机器学习中解决这个问题需要通过与模型相关联的结构化表格数据来学习某种表示,这在以前是通过统计测量或核函数来进行的。近年来趋势已经转向对图进行编码以生成嵌入向量来训练机器学习模型。
机器学习模型的目标是训练机器在数据集中大规模学习和模式识别。在处理图时这一点会被放大,因为图提供不同而复杂的结构,这是其他形式的数据(如文本、音频或图像)所不具备的。基于图的机器学习可以检测并解释重复出现的潜在模式[2]。
我们可能对确定与社交网络上的用户相关的人口统计信息感兴趣。人口统计数据包括年龄、性别、种族等。像Facebook或Twitter这样的公司的社交媒体网络范围从数百万-数十亿的用户和数万亿的边。肯定会有几个与该网络中用户的人口统计信息相关的模式,这些模式不容易通过人类或算法检测到,但模型应该能够学习它们。类似地,我们可能想推荐一对用户成为朋友,而他们目前还不是朋友。这就为链接预测(基于图的机器学习的另一个应用)提供了素材。
什么是图嵌入?
特征工程是指处理输入数据形成一组特征的常用方法,这些特征提供了原始数据集的紧凑且有意义的表示。特征工程阶段的结果将作为机器学习模型的输入。这是在表格结构化数据集的处理时必备的过程,但在处理图数据时却是一种难以执行的方法,因为需要找到一种方法来生成与所有图数据相关联的合适表示。
有多种方法可以从图中生成表示结构信息的特征。最常见和最直接的方法是从图中提取统计数据。这可以包括识别度分布、page rank、centrality metrics、jaccard 分数等。然后通过内核函数将所需属性合并到模型中,但是核函数的问题是生成结果的相关时间复杂度很高。
最近的研究趋势已经转向寻找有意义的图表示,对图生成嵌入表示。这些嵌入学习了保持网络原始结构的图表示。我们可以将其视为旨在将离散图转换为连续域的映射函数。一旦学习了函数,就可以将其应用于图,并且生成的映射可以用作机器学习算法的特征集 。
图嵌入的类型
对图的分析可以分解为 3 个粒度级别。节点级别、边缘级别和图级别(整个图)。每个级别由生成嵌入向量的不同过程组成,所选过程应取决于正在处理的问题和数据。下面介绍的每个粒度级别的嵌入都有附图来直观地彼此不同。
节点嵌入
在节点级别,生成与图中的每个节点关联的嵌入向量。这个嵌入向量可以容纳图的表示和结构。本质上说彼此接近的节点也应该有彼此接近的向量。这是流行的节点嵌入模型(如Node2Vec)的基本原则之一。
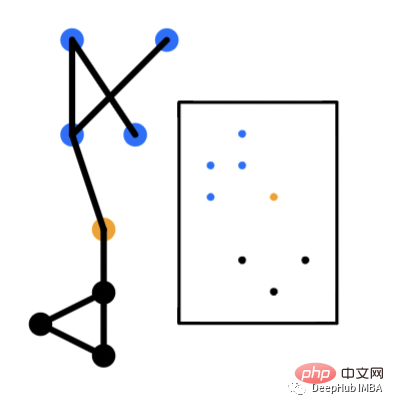
边嵌入
在边缘层中,生成一个与图中的每条边相关的嵌入向量。链路预测问题是使用边嵌入的一个常见应用。链接预测是指预测一对节点之间是否有一条边连接的可能性。这些嵌入可以学习图提供的边属性。例如在一个社交网络图中,可以有一个多边图,其中节点可以根据年龄范围、性别等用边连接。表示该边的相关向量可以学习这些边属性。
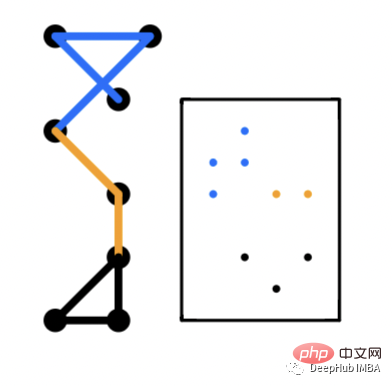
图嵌入
图级别的嵌入并不常见,它们包括生成一个表示每个图的嵌入向量。例如一个有多个子图的大图,每个对应的子图都有一个表示图结构的嵌入向量。分类问题是图嵌入可能有用的常见应用。这些类型的问题将包括将图分类到特定类别。
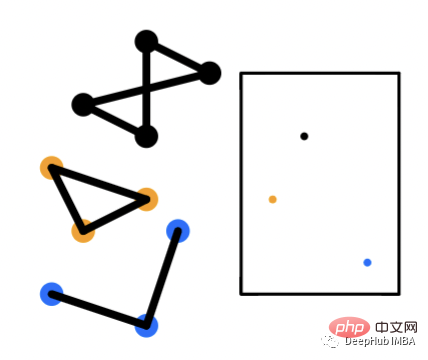
Python实现
使用python代码实现我们需要以下的这些库
Pythnotallow=3.9 networkx>=2.5 pandas>=1.2.4 numpy>=1.20.1 node2vec>=0.4.4 karateclub>=1.3.3 matplotlib>=3.3.4
如果您没有安装node2vec包,请参考它的文档。安装karateclub包,也类似
节点嵌入
import random
import networkx as nx
import matplotlib.pyplot as plt
from node2vec import Node2Vec
from node2vec.edges import HadamardEmbedder
from karateclub import Graph2Vec
plt.style.use("seaborn")
# generate barbell network
G = nx.barbell_graph(
m1 = 13,
m2 = 7
)
# node embeddings
def run_n2v(G, dimensions=64, walk_length=80, num_walks=10, p=1, q=1, window=10):
"""
Given a graph G, this method will run the Node2Vec algorithm trained with the
appropriate parameters passed in.
Args:
G (Graph) : The network you want to run node2vec on
Returns:
This method will return a model
Example:
G = np.barbell_graph(m1=5, m2=3)
mdl = run_n2v(G)
"""
mdl = Node2Vec(
G,
dimensions=dimensions,
walk_length=walk_length,
num_walks=num_walks,
p=p,
q=q
)
mdl = mdl.fit(window=window)
return mdl
mdl = run_n2v(G)
# visualize node embeddings
x_coord = [mdl.wv.get_vector(str(x))[0] for x in G.nodes()]
y_coord = [mdl.wv.get_vector(str(x))[1] for x in G.nodes()]
plt.clf()
plt.scatter(x_coord, y_coord)
plt.xlabel("Dimension 1")
plt.ylabel("Dimension 2")
plt.title("2 Dimensional Representation of Node2Vec Algorithm on Barbell Network")
plt.show()
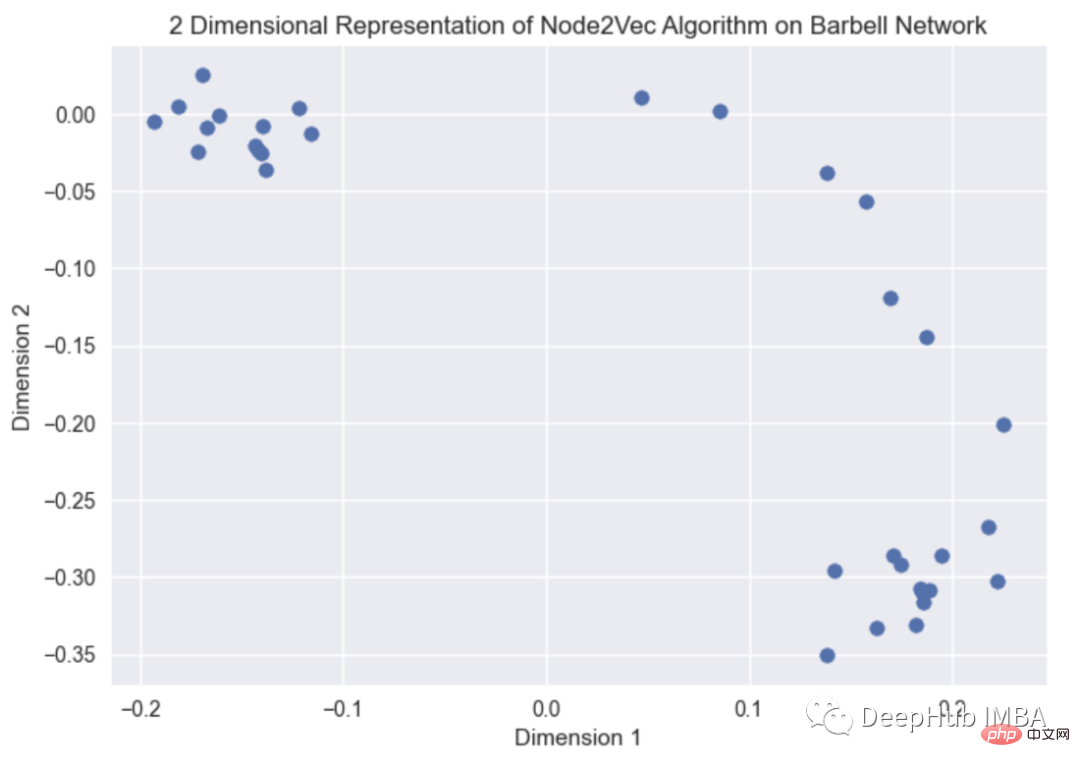
上图是由barbell graph 生成的节点嵌入可视,有许多计算节点嵌入的方法,如node2vec、deep walk、random walks等。这里使用node2vec。
边嵌入
edges_embs = HadamardEmbedder(
keyed_vectors=mdl.wv
)
# visualize embeddings
coordinates = [
edges_embs[(str(x[0]), str(x[1]))] for x in G.edges()
]
plt.clf()
plt.scatter(coordinates[0], coordinates[1])
plt.xlabel("Dimension 1")
plt.ylabel("Dimension 2")
plt.title("2 Dimensional Representation of Edge Embeddings on Barbell Network")
plt.show()
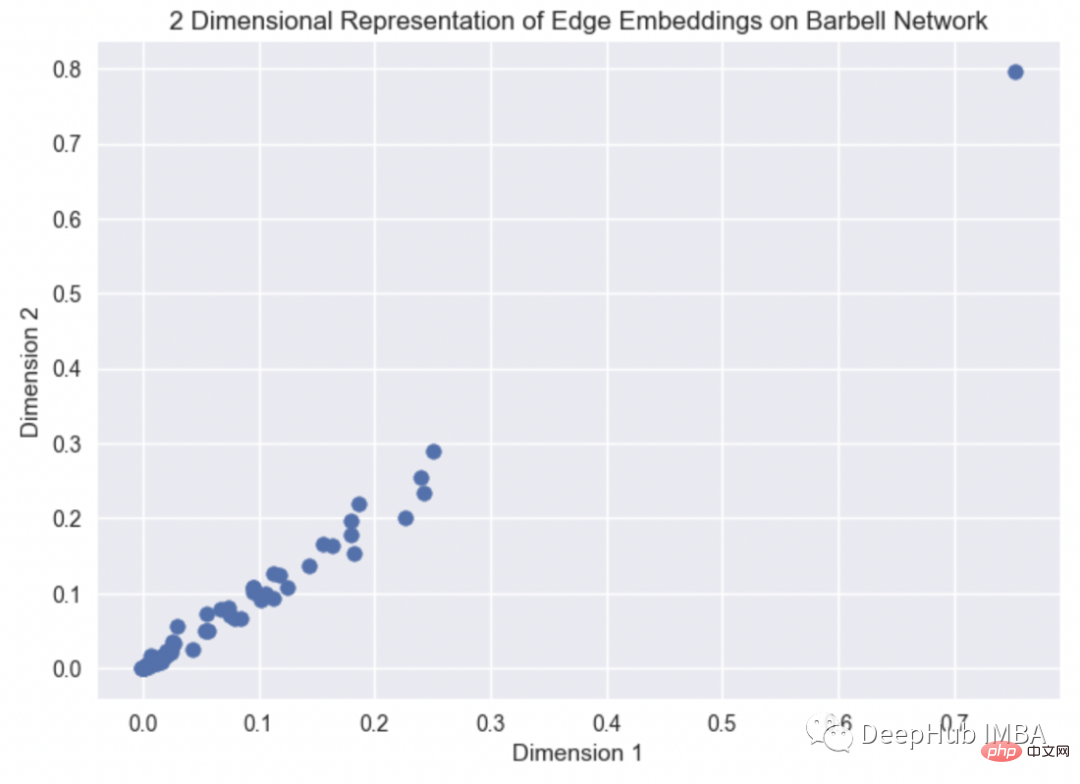
通过barbell graph查看边嵌入的可视化,Hammard Embedder的源代码可以在这里找到(https://github.com/eliorc/node2vec/blob/master/node2vec/edges.py#L91)。
图嵌入
n_graphs = 10
Graphs = [
nx.fast_gnp_random_graph(
n = random.randint(5,15),
p = random.uniform(0,1)
) for x in range(n_graphs)
]
g_mdl = Graph2Vec(dimensions=2)
g_mdl.fit(Graphs)
g_emb = g_mdl.get_embedding()
x_coord = [vec[0] for vec in g_emb]
y_coord = [vec[1] for vec in g_emb]
plt.clf()
plt.scatter(x_coord, y_coord)
plt.xlabel("Dimension 1")
plt.ylabel("Dimension 2")
plt.title("2 Dimensional Representation of Graph Embeddings on Randomly Generated Networks")
plt.show()
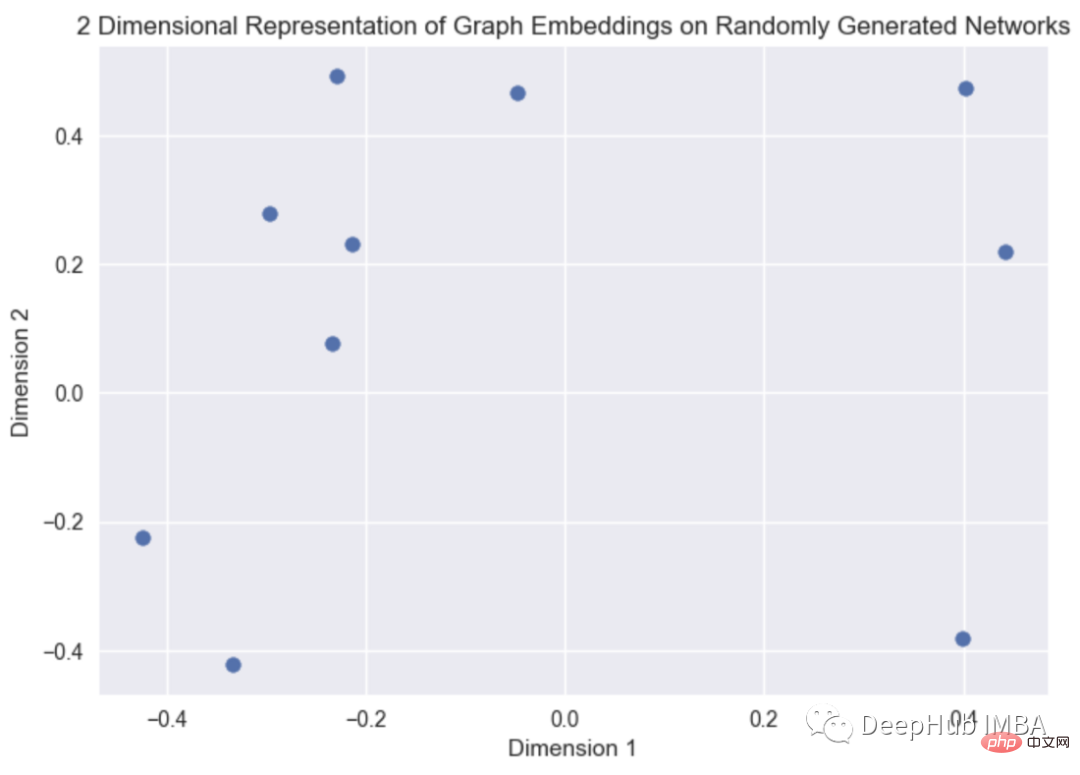
这是一个由随机生成的图的图嵌入可视化,graph2vec算法的源代码可以在这里找到。(https://karateclub.readthedocs.io/en/latest/_modules/karateclub/graph_embedding/graph2vec.html)
总结
嵌入是一个将离散图映射到向量表示的函数。从图数据中可以生成多种形式的嵌入,节点嵌入、边嵌入和图嵌入。所有三种类型的嵌入都提供了一种向量表示,将图的初始结构和特征映射到X维的数值。































