Python语言实现线性回归的步骤有:导入所要用到的库,读取数据并进行预处理。分析数据以及建立线性回归模型,并进行模型训练检验模型效果
通过使用python语言来实现线性回归是非常方便的,因为它提供了多个现成的库,比如可以使用numpy.linalog.lstsq,pandas.ols以及
scipy.stats.linregress等,在本文中将使用sklearn库的linear_model.LinearRegression,它支持任意维度,非常好用。
立即学习“Python免费学习笔记(深入)”;
【推荐教程:Python教程】
二维直线
例:线性方程y=a∗x+b;y=a∗x+b 表示平面一直线
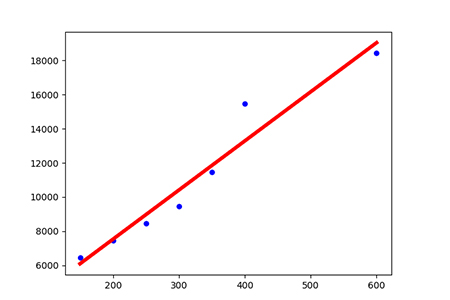
在下面的例子中,我们将建立线性回归模型,通过给出房屋的面积来预测房屋的价格
import pandas as pd from io import StringIO from sklearn import linear_model import matplotlib.pyplot as plt # 房屋面积与价格历史数据(csv文件) csv_data = 'square_feet,price\n150,6450\n200,7450\n250,8450\n300,9450\n350,11450\n400,15450\n600,18450\n' # 读入dataframe df = pd.read_csv(StringIO(csv_data)) print(df) # 建立线性回归模型 regr = linear_model.LinearRegression() # 拟合 regr.fit(df['square_feet'].reshape(-1, 1), df['price']) # 注意此处.reshape(-1, 1),因为X是一维的! # 不难得到直线的斜率、截距 a, b = regr.coef_, regr.intercept_ # 给出待预测面积 area = 238.5 # 方式1:根据直线方程计算的价格 print(a * area + b) # 方式2:根据predict方法预测的价格 print(regr.predict(area)) # 画图 # 1.真实的点 plt.scatter(df['square_feet'], df['price'], color='blue') # 2.拟合的直线 plt.plot(df['square_feet'], regr.predict(df['square_feet'].reshape(-1,1)), color='red', linewidth=4) plt.show()
效果图:
三维平面
线性方程z=a∗x+b∗y+c;z=a∗x+b∗y+c 表示空间一平面
import numpy as np from sklearn import linear_model from mpl_toolkits.mplot3d import Axes3D import matplotlib.pyplot as plt xx, yy = np.meshgrid(np.linspace(0,10,10), np.linspace(0,100,10)) zz = 1.0 * xx + 3.5 * yy + np.random.randint(0,100,(10,10)) # 构建成特征、值的形式 X, Z = np.column_stack((xx.flatten(),yy.flatten())), zz.flatten() # 建立线性回归模型 regr = linear_model.LinearRegression() # 拟合 regr.fit(X, Z) # 不难得到平面的系数、截距 a, b = regr.coef_, regr.intercept_ # 给出待预测的一个特征 x = np.array([[5.8, 78.3]]) # 方式1:根据线性方程计算待预测的特征x对应的值z(注意:np.sum) print(np.sum(a * x) + b) # 方式2:根据predict方法预测的值z print(regr.predict(x)) # 画图 fig = plt.figure() ax = fig.gca(projection='3d') # 1.画出真实的点 ax.scatter(xx, yy, zz) # 2.画出拟合的平面 ax.plot_wireframe(xx, yy, regr.predict(X).reshape(10,10)) ax.plot_surface(xx, yy, regr.predict(X).reshape(10,10), alpha=0.3) plt.show()
效果图:

总结:以上就是本篇文章的全部内容了,希望对大家有所帮助































