多目标跟踪之卡尔曼滤波

3 卡尔曼滤波眼里的行人跟踪问题

• 下面是图例公式的描述,初学同学可能有点蒙，建议去查一下卡尔曼滤波相关视频（然后发现还是蒙/坏笑/,但每次的学习都会有新的发现/加油/）
• 下面是UP学习了不错文章作者Bzarg

• 一个包含位置信息和速度信息的状 x=（p,v）

• 卡尔曼滤波假设两个变量（在我们的例子里是位置和速度）都应该是随机的，而且符合高斯分布。如下图 

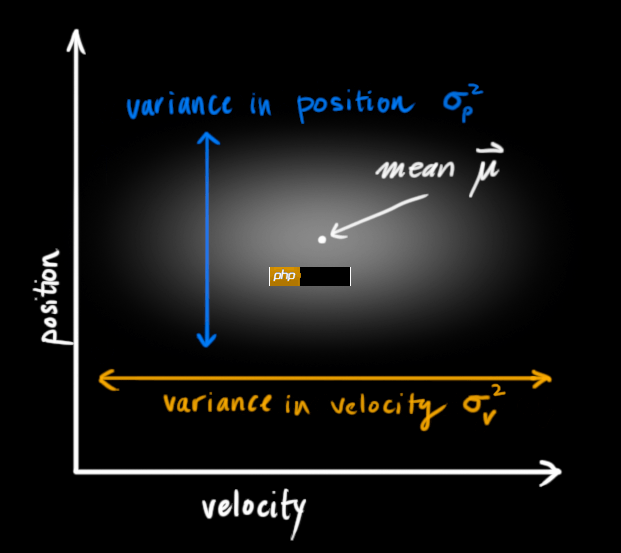
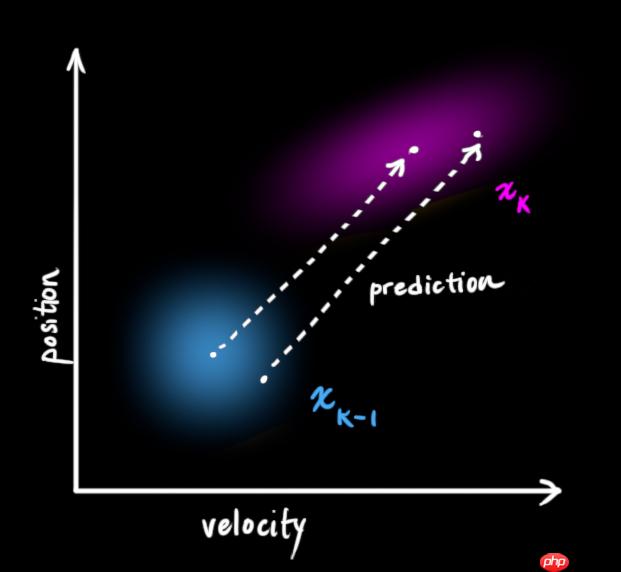
• 位置和速度是不相关的，这意味着我们不能从一个变量推测另一个变量。那么如果位置和速度相关呢？如下图所示，人前往特定位置的可能性取决于它拥有的速度。

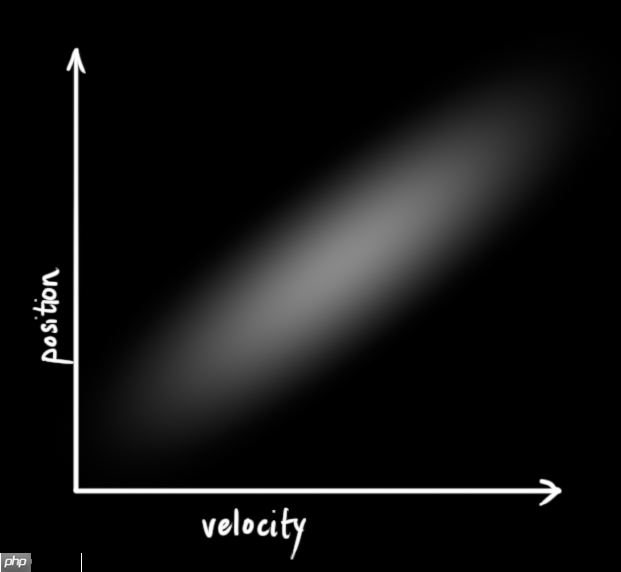
• 这不难理解，如果基于旧位置估计新位置，我们会产生这两个结论：如果速度很快，人可能移动得更远，所以得到的位置会更远；如果速度很慢，人就走不了那么远。

• 这种关系对目标跟踪来说非常重要，因为它提供了更多信息：一个可以衡量可能性的标准。这就是卡尔曼滤波的目标：从不确定信息中挤出尽可能多的信息！

• 为了捕获这种相关性，我们用的是协方差矩阵。简而言之，矩阵的每个值是第i个变量和第j个变量之间的相关程度（由于矩阵是对称的，i和j的位置可以随便交换）。我们用表示协方差矩阵，在这个例子中，就是。

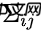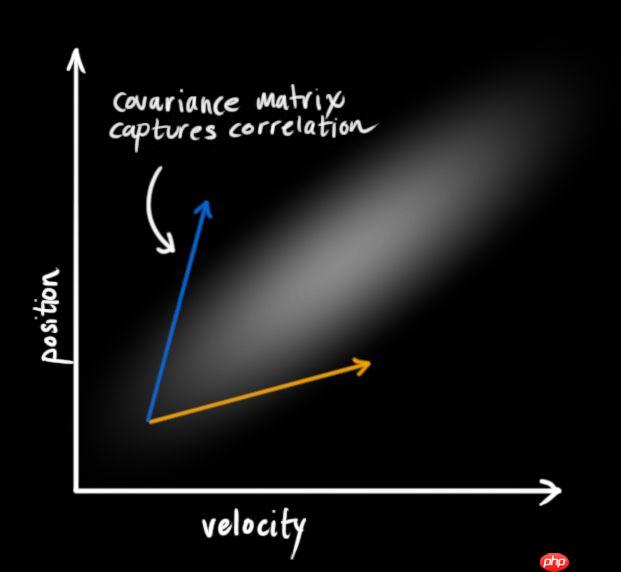
• 为了把以上关于状态的信息建模为高斯分布（图中色块），我们还需要k时的两个信息：最佳估计（均值，也就是，协方差矩阵。（虽然还是用了位置和速度两个变量，但只要和问题相关，卡尔曼滤波可以包含任意数量的变量）

• 接下来，我们要通过查看当前状态（k-1时）来预测下一个状态（k时）。这里我们查看的状态不是真值，但预测函数无视真假，可以给出新分布：

我们可以用矩阵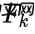表示这个预测步骤：

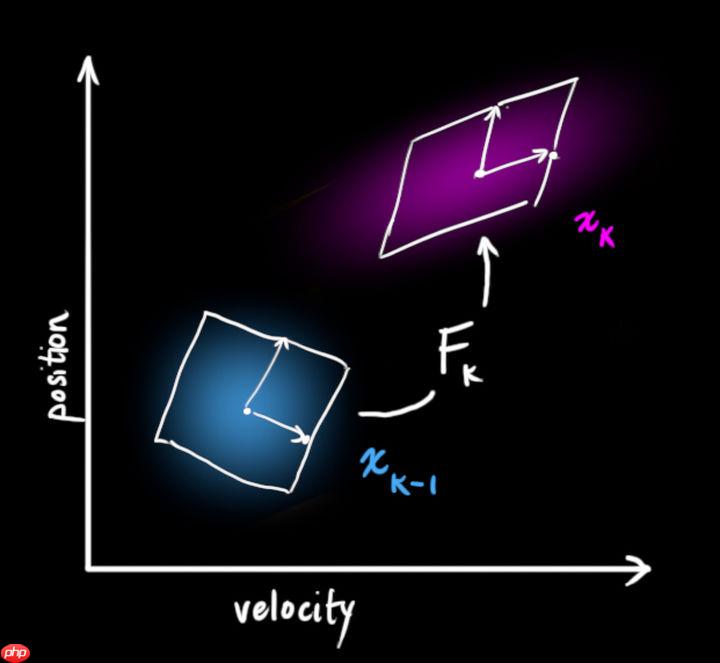
• 它从原始预测中取每一点，并将其移动到新的预测位置。如果原始预测是正确的，系统就会移动到新位置。这是怎么做到的？为什么我们可以用矩阵来预测人下一刻的位置和速度？下面是个简单公式：

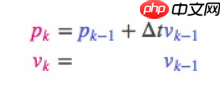
• 换成矩阵形式：

• 这是一个预测矩阵，它能给出人的下一个状态，但目前我们还不知道协方差矩阵的更新方法。这也是我们要引出下面这个等式的原因：如果我们将分布中的每个点乘以矩阵A，那么它的协方差矩阵会发生什么变化

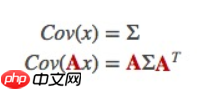
把这个式子和上面的最佳估计 结合，可得：

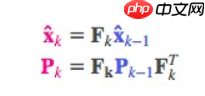
• 外部影响
• 但是，除了速度和位置，外因也会对系统造成影响。比如模拟火车运动，除了列车自驾系统，列车操作员可能会手动调速。在我们的机器人示例中，导航软件也可以发出停止指令。对于这些信息，我们把它作为一个向量，纳入预测系统作为修正。假设油门设置和控制命令是已知的，我们知道火车的预期加速度a。根据运动学基本定理，我们可得：

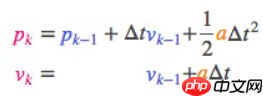
• 把它转成矩阵形式：

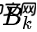• 是控制矩阵，是控制向量。如果外部环境异常简单，我们可以忽略这部分内容，但是如果添加了外部影响后，模型的准确率还是上不去，这又是为什么呢？

• 外部不确定性

• 但是，如果存在我们不知道的力量呢？当我们监控无人机时，它可能会受到风的影响；当我们跟踪轮式机器人时，它的轮胎可能会打滑，或者粗糙地面会降低它的移速。这些因素是难以掌握的，如果出现其中的任意一种情况，预测结果就难以保障。这要求我们在每个预测步骤后再加上一些新的不确定性，来模拟和“世界”相关的所有不确定性：

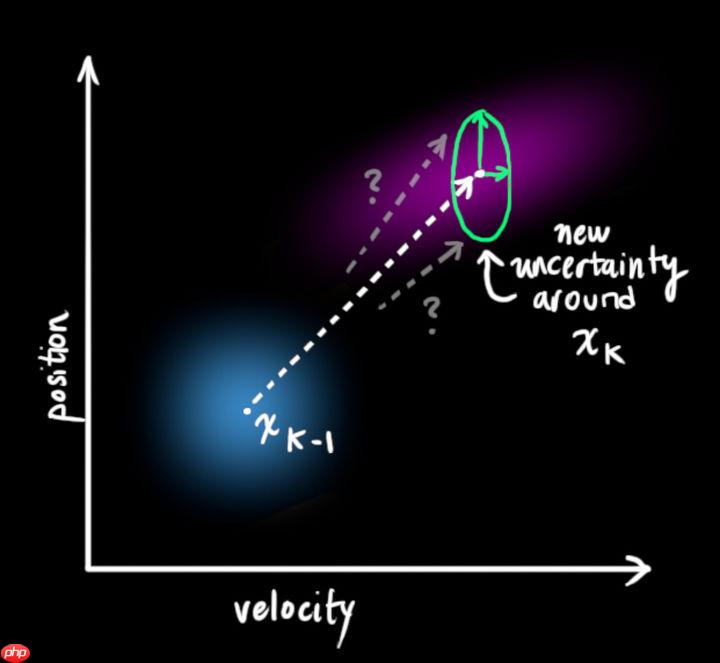
• 如上图所示，加上外部不确定性后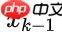，的每个预测状态都可能会移动到另一点，也就是蓝色的高斯分布会移动到紫色高斯分布的位置，并且具有协方差。换句话说，我们把这些不确定影响视为协方差的噪声。

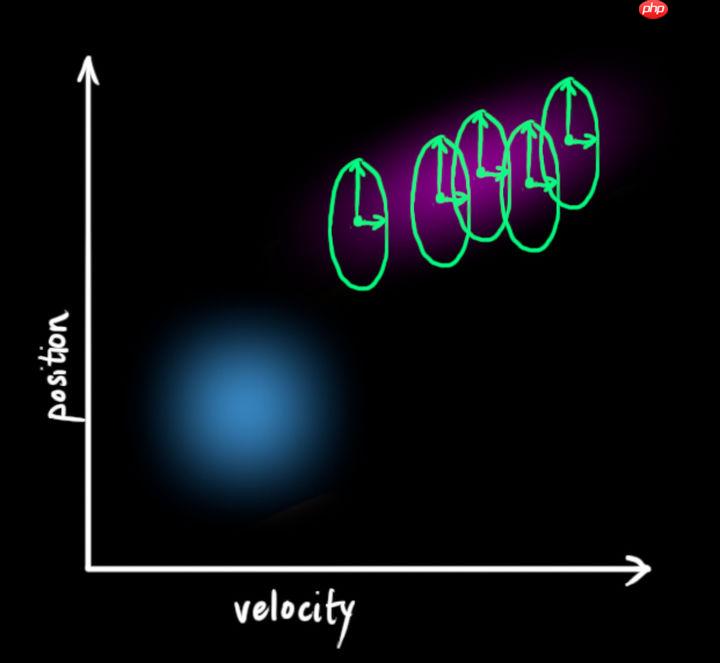
• 这个紫色的高斯分布拥有和原分布相同的均值，但协方差不同。

PDFlux

PDF内容提取+智能问答神器，结合了科研级精准的非结构化文档解析能力，以及ChatGPT的智能问答能力。

下载

我们在原式上加入

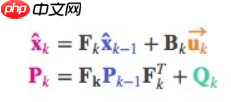
• 新的最佳估计是基于原最佳估计和已知外部影响矫正后得到的预测
• 新的不确定性是基于原不确定性和外部环境不确定性得到的预测

• 通过测量来细化估计值

• 我们可能有好几个传感器，它们一起提供有关系统状态的信息。传感器的作用不是我们关心的重点，它可以读取位置，可以读取速度，重点是，它能告诉我们关于状态的间接信息——它是状态下产生的一组读数。

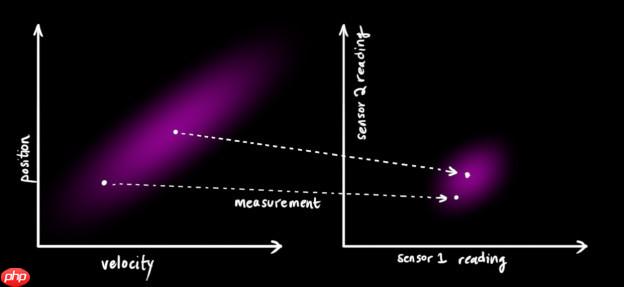
• 请注意，读数的规模和状态的规模不一定相同，所以我们把传感器读数矩阵设为

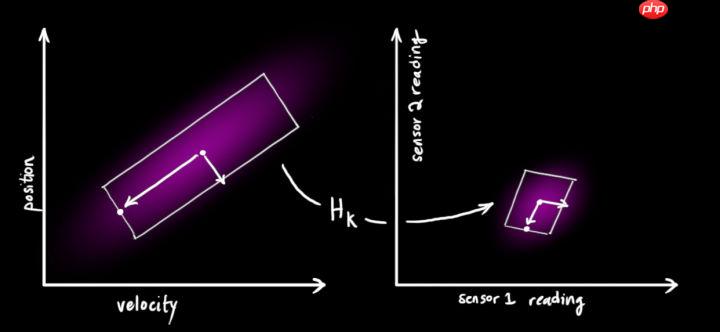
• 把这些分布转换为一般形式

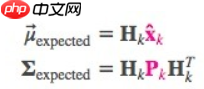
• 卡尔曼滤波的一大优点是擅长处理传感器噪声。换句话说，由于种种因素，传感器记录的信息其实是不准的，一个状态事实上可以产生多种读数。

• 我们将这种不确定性（即传感器噪声）的协方差设为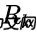，读数的分布均值设为。现在我们得到了两块高斯分布，一块围绕预测的均值，另一块围绕传感器读数。

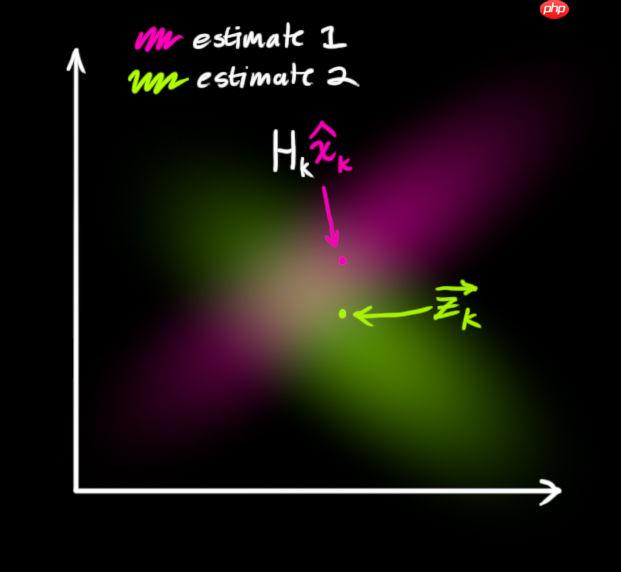
• 如果要生成靠谱预测，模型必须调和这两个信息。也就是说，对于任何可能的读数，这两种方法预测的状态都有可能是准的，也都有可能是不准的。重点是我们怎么找到这两个准确率。最简单的方法是两者相乘：

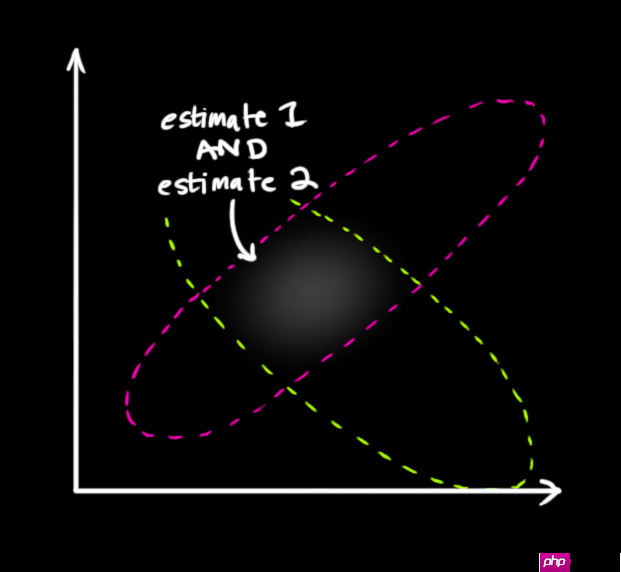
• 两块高斯分布相乘后，我们可以得到它们的重叠部分，这也是会出现最佳估计的区域。换个角度看，它看起来也符合高斯分布：

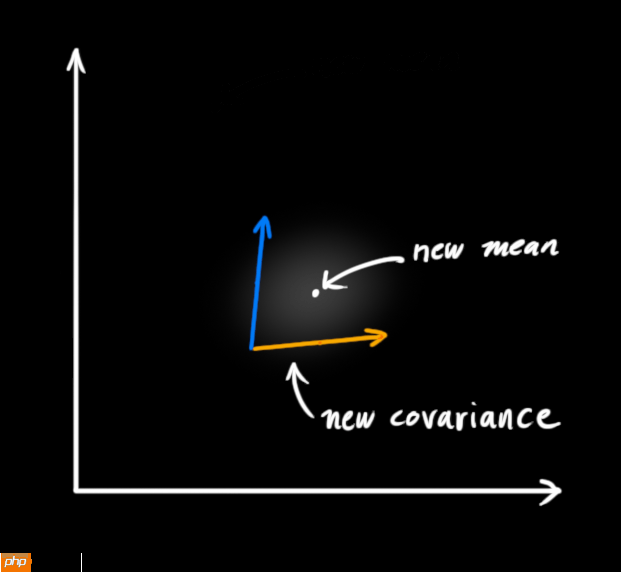
• 事实证明，当你把两个高斯分布和它们各自的均值和协方差矩阵相乘时，你会得到一个拥有独立均值和协方差矩阵的新高斯分布。最后剩下的问题就不难解决了：我们必须有一个公式来从旧的参数中获取这些新参数！

• 结合高斯

• 两条高斯曲线相乘

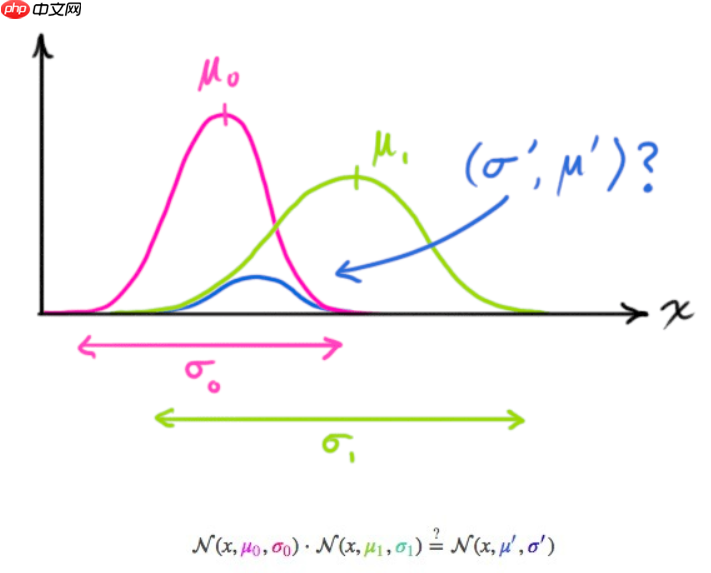
• 按照一维方程进行扩展，可得

• 用k简化一下

• 以上是一维的内容，如果是多维空间，把这个式子转成矩阵格式

• 这个矩阵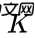就是我们说的卡尔曼增益
• 结合在一起
• 截至目前，我们有用矩阵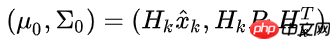预测的分布，有用传感器读数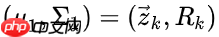预测的分布。把它们代入上节的矩阵等式中：

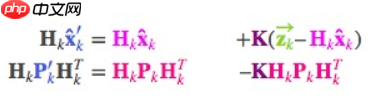
• 相应的，卡尔曼增益就是：

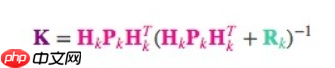
考虑到里还包含着一个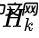，我们再精简一下上式

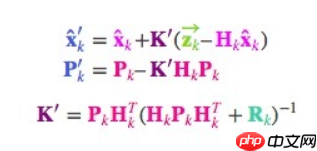
最后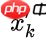，是我们的最佳估计值，我们可以把它继续放进去做另一轮预测

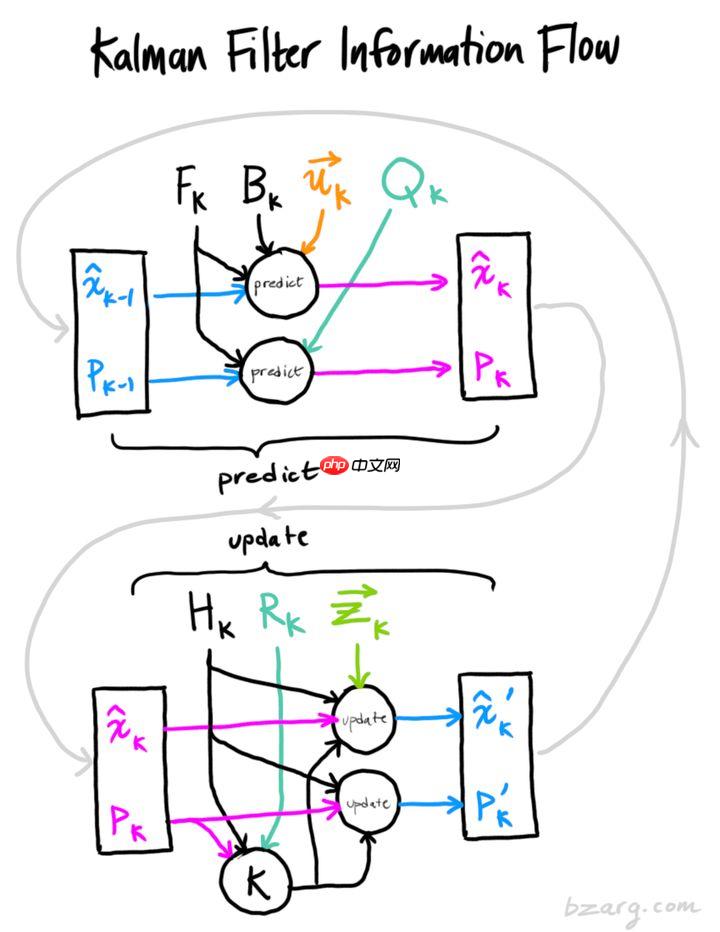
4 代码实现

import matplotlib.pyplot as plt# 模拟数据t = np.linspace(1,100,100)# print(t)a = 0.5position = (a * t**2)/2# print(position)position_noise = position+np.random.normal(0,120,size=(t.shape[0])) 

plt.plot(t,position,label='truth position')  # 原值plt.plot(t,position_noise,label='only use measured position')  # 加入噪声的值# 初始的估计的位置就直接用GPS测量的位置predicts = [position_noise[0]]
position_predict = predicts[0]

predict_var = 0odo_var = 120**2 #这是我们自己设定的位置测量仪器的方差，越大则测量值占比越低v_std = 50 # 测量仪器的方差for i in range(1,t.shape[0]):
  
    dv =  (position[i]-position[i-1]) + np.random.normal(0,50) # 模拟从惯性测量单元IMU读取出的速度
    position_predict = position_predict + dv # 利用上个时刻的位置和速度预测当前位置
    predict_var += v_std**2 # 更新预测数据的方差
    # 下面是Kalman滤波
    position_predict = position_predict*odo_var/(predict_var + odo_var)+position_noise[i]*predict_var/(predict_var + odo_var)
    predict_var = (predict_var * odo_var)/(predict_var + odo_var)**2
    predicts.append(position_predict)

    
plt.plot(t,predicts,label='kalman filtered position')  # 滤波后的值plt.legend()
plt.show()# 卡尔曼滤波将噪声值（橙色线），滤波后（绿色线），尽量去拟合原值（蓝色线）