数学期望作为概率论与统计学的基础概念,体现了随机变量平均值的大小,是衡量随机现象的重要指标。
- 数学期望的基本计算公式可参考以下内容。
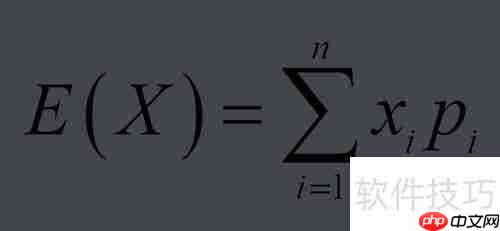
- 对于离散型随机变量,其数学期望的定义及公式如下所示。

- 在处理问题时,需明确各事件的发生概率,通过细致分析事件特性来预测结果。
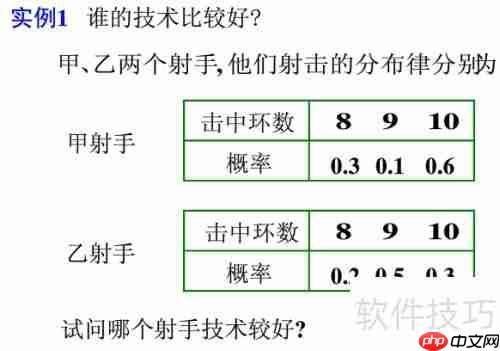
- 接下来,确定每个事件发生的概率,并将其与对应的结果相乘,最后将所有乘积求和,就能得出期望值。


MATLAB(矩阵实验室)是MATrix LABoratory的缩写,是一款由美国The MathWorks公司出品的商业数学软件。MATLAB是一种用于算法开发、数据可视化、数据分析以及数值计算的高级技术计算语言和交互式环境。除了矩阵运算、绘制函数/数据图像等常用功能外,MATLAB还可以用来创建用户界面及与调用其它语言(包括C,C++和FORTRAN)编写的程序。MATLAB基础知识;命令窗口是用户与MATLAB进行交互作业的主要场所,用户输入的MATLAB交互命令均在命令窗口执行。 感兴趣的朋友可以
- 在实际应用中,我们常用符号X表示事件可能的状态,P表示相应概率,而所有事件的概率总和恒等于1,这就是离散型随机变量的核心思想。
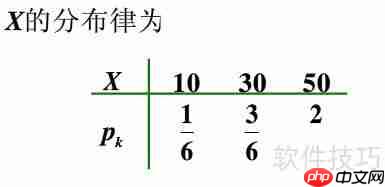
- 对于连续型随机变量,其数学期望的计算遵循以下公式。

- 若随机变量呈现指数分布,则属于连续型随机变量的一种特殊情况,在考试中涉及的概率相对较低,考生可以适度掌握相关知识。



























