2493。将节点分为最大组
>难度: hard
>主题:广度优先搜索,联合查找,图形
>给您一个正整数n,代表无向图中的节点的数量。节点从1到n。 >您还会给您一个2d整数数组边缘,其中边缘[i] = [a
i,bi>]表示存在bivecrectional 节点ai 和bi之间的边缘。 通知可以断开给定的图。> 将图的节点划分为m组(
1个索引),这样的节点是:>
图中的每个节点完全属于一个组。- >
- 对于图中的每个节点,由边缘连接的[a i
- ,b i]使用索引x,bi属于索引y的组,然后| y -x | = 1.返回>您可以将节点划分的最大组数(即最大值)。返回 -1如果不可能将节点与给定条件
分组
>>示例1:
>输入:
- 4
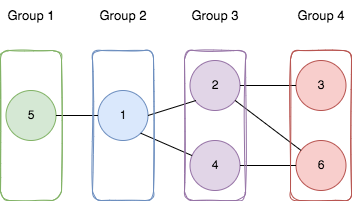
- >说明: >如图所示:
- >将节点5添加到第一个组。 >将节点1添加到第二组。
-
>将节点2和4添加到第三组。
- >将节点3和6添加到第四组。
- > 我们可以看到每个边缘都可以满足。
- >可以证明,如果我们创建第五组并将任何节点从第三或第四组移动到其中,那么至少在边缘上都无法满足。
- >
- > >示例2:
>输入:
>输出:
-1- >说明:如果将节点1添加到第一个组,将节点2添加到第二组中,然后将节点3添加到第三组以满足前两个边缘,我们可以看到,第三个边缘将不满足第三个边缘。
- 可以证明不可能分组。
-
>约束:
- >
edges [i] .length == 2
- 1 i
- ,b i
- a i
- != bi> 在任何一对顶点之间最多都有一个边缘。 >
- 提示:
- 如果图不是双分,则不可能分组节点。
>请注意,我们可以独立解决每个连接的组件的问题,最终答案将只是每个组件中最大组的总数。 >
>最后,要解决每个连接的组件的问题,我们可以注意到,如果对于某个节点v,我们将其位置固定在最左边的组中,那么我们也可以评估其他每个节点的位置。该位置是扎根在节点v。
解决方案:- 问题,
- “将节点分为最大组数” ,涉及确定可以将无向图的节点划分为:
- 的最大组数。
组成的索引恰好有1个。 如果该图不是双分部分,则不可能进行分组,并且该函数必须返回-1。
>关键点
- 图形属性:
- 该图可以断开连接。 >
- >验证:
>二分性质:
解决方案涉及bfs以验证双方。- 联合 - 芬德:有效地分组连接的组件。>
- 方法
- 预处理:
- 使用邻接列表表示图形。
>使用union-find来识别连接的组件。
-
bfs验证两肢:
对于每个连接的组件,请使用bfs确定它是否为双分。> - 如果不是双分,请返回-1。
>计算组计数: -
对于每个连接的组件,使用bfs确定最大深度,代表组的最大数量。
- 组合结果:
>
- 组合结果:
-
计划 - >使用union-find对组连接的组件。
图中每个节点的>:
>使用bfs检查图形是否是双分部分,并计算该组件的最大深度。
>让我们在php中实现此解决方案: 2493。将节点划分为最大组数>
-
解释:
- 1。 union-find类
-
- > union-find(不连接集合联合)结构将节点组为连接的组件,并执行两个主要任务:
find: - >标识节点连接的组件的根。
>根据等级合并两个连接的组件。
>二分化验证:
使用bfs,为节点分配交替的“颜色”。如果相邻的节点共享相同的颜色,则该图不是两部分。>
- >深度计算:
- >测量bfs树的深度以确定组的最大数量。 3。结合结果
- 计算每个连接的组件的最大深度。
添加所有组件的深度以确定结果。
示例演练- >示例1
- 输入:
$n = 6; $edges = [[1,2], [1,4], [1,5], [2,6], [2,3], [4,6]];步骤:
>构造邻接列表:
1 -> [2, 4, 5] 2 -> [1, 3, 6] 3 -> [2] 4 -> [1, 6] 5 -> [1] 6 -> [2, 4]
所有组件中的总和深度:4。
>输出:4
>示例2
输入:
$n = 3; $edges = [[1,2], [2,3], [3,1]];
步骤:
- >构造邻接列表:
1 -> [2, 3] 2 -> [1, 3] 3 -> [1, 2]
- 使用bfs:
- 组件1:不是双方。
- >输出:-1
时间复杂度
图形结构:

专为中小型企业定制的网络办公软件,富有竞争力的十大特性: 1、独创 web服务器、数据库和应用程序全部自动傻瓜安装,建立企业信息中枢 只需3分钟。 2、客户机无需安装专用软件,使用浏览器即可实现全球办公。 3、集成Internet邮件管理组件,提供web方式的远程邮件服务。 4、集成语音会议组件,节省长途话费开支。 5、集成手机短信组件,重要信息可直接发送到员工手机。 6、集成网络硬
o(e)
- ,其中
- e
- 是边缘的数量。 >
>联合 - find:
o(α(n)) ,其中
-
n
是节点的数量(由于路径压缩而几乎恒定)。 bfs:o(v e) ,其中 - v 是顶点的数量。 总体复杂性:o(n e)>
-
>输出示例
$n = 6; $edges = [[1,2], [1,4], [1,5], [2,6], [2,3], [4,6]]; echo magnificentSets($n, $edges); // Output: 4 $n = 3; $edges = [[1,2], [2,3], [3,1]]; echo magnificentSets($n, $edges); // Output: -1
这种方法通过利用bfs进行两性检查和深度计算来有效地处理分组问题,同时利用union-find来简化组件管理。该解决方案处理连接和断开的图形。 联系链接 如果您发现此系列有帮助,请考虑在github上给出reposority cository >在您喜欢的社交网络上分享帖子。您的支持对我来说意义重大!> 如果您想要这样的更多有用的内容,请随时关注我:>
github





























